Clustering using the Bisecting K-Means algorithmm (SPMF documentation)
This example explains how to run the Bisecting K-Means algorithm using the SPMF open-source data mining library.
How to run this example?
- If you are using the graphical interface, (1)
choose the "BisectingKMeans" algorithm, (2) select the input file "inputDBScan2.txt",
(3) set the output file name (e.g. "output.txt")
(4) set k =3, distance function = euclidian, iter = 10 and(5) click "Run algorithm".
Note that there is also an optional parameter called "separator". It can be used to read other types of input files where values are not separated by spaces. For example, for a file separated by the ',' character, the parameter "separator" would have to be set to ",".
- If you want to execute this example from the command line,
then execute this command:
java -jar spmf.jar run BisectingKMeans inputDBScan2.txt output.txt 3 euclidian 10 in a folder containing spmf.jar and the example input file inputDBScan2.txt. - If you are using the source code version of SPMF, launch the file "MainTestBisectingKMeans_saveToFile.java" in the package ca.pfv.SPMF.tests.
What is Bisecting K-Means?
K-Means is one of the most famous clustering algorithm. It is used to separate a set of instances (vectors of double values) into groups of instances (clusters) according to their similarity.
The Bisecting K-Means algorithm is a variation of the regular K-Means algorithm that is reported to perform better for some applications. It consists of the following steps: (1) pick a cluster, (2) find 2-subclusters using the basic K-Means algorithm, * (bisecting step), (3) repeat step 2, the bisecting step, for ITER times and take the split that produces the clustering, (4) repeat steps 1,2,3 until the desired number of clusters is reached.
In this implementation the user can choose between various distance functions to assess the distance between vectors. SPMF offers the Euclidian distance, correlation distance, cosine distance, Manathan distance and Jaccard distance.
What is the input?
Bisecting K-Means takes as input a set of instances (each having a name and containing one or more double values), a parameter K (a positive integer >=1) indicating the number of clusters to be created, a distance function, and the parameter ITER.
The input file format of K-Means is a text file containing several instances.
The first lines (optional) specify the name of the attributes used for describing the instances. In this example, two attributes will be used, named X and Y. But note that more than two attributes could be used. Each attribute is specified on a separated line by the keyword "@ATTRIBUTEDEF=", followed by the attribute name
Then, each instance is described by two lines. The first line (which is optional) contains the string "@NAME=" followed by the name of the instance. Then, the second line provides a list of double values separated by single spaces.
An example of input is provided in the file "inputDBScan2.txt" of the SPMF distribution. It contains 31 instances, each described by two attribute called X and Y.
@ATTRIBUTEDEF=X
@ATTRIBUTEDEF=Y
@NAME=Instance1
1 1
@NAME=Instance2
0 1
@NAME=Instance3
1 0
@NAME=Instance4
11 12
@NAME=Instance5
11 13
@NAME=Instance6
13 13
@NAME=Instance7
12 8.5
@NAME=Instance8
13 8
@NAME=Instance9
13 9
@NAME=Instance10
13 7
@NAME=Instance11
11 7
@NAME=Instance12
8 2
@NAME=Instance13
9 2
@NAME=Instance14
10 1
@NAME=Instance15
7 13
@NAME=Instance16
5 9
@NAME=Instance17
16 16
@NAME=Instance18
11.5 8
@NAME=Instance20
13 10
@NAME=Instance21
12 13
@NAME=Instance21
14 12.5
@NAME=Instance22
14.5 11.5
@NAME=Instance23
15 10.5
@NAME=Instance24
15 9.5
@NAME=Instance25
12 9.5
@NAME=Instance26
10.5 11
@NAME=Instance27
10 10.5
@NAME=Instance28
9 3
@NAME=Instance29
9 4
@NAME=Instance30
9 5
For example, the first instance is named "Instance1", and it is a vector with two values: 1 and 1 for the attributes X and Y, respectively.
This input file represents a set of 2D points. But note that, it is possible to use more than two attributes to describe instances. To give a better idea of what the input file looks like, here is a visual representation:
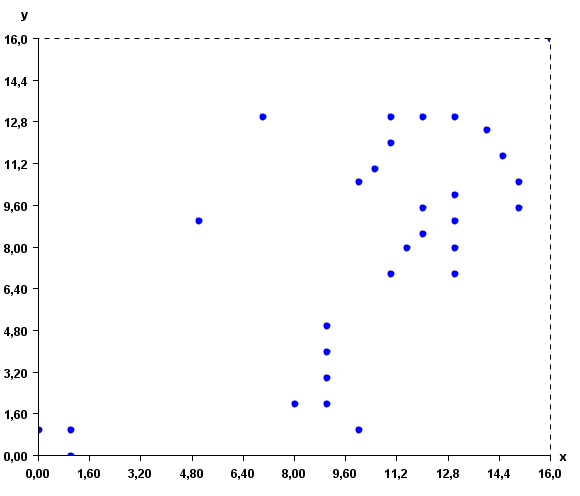
The Bisecting K-Means algorithm will group the instances according to their similarity. To do this, it is also necessary to specify the distance function to be used for comparing the instances. The distance function can be the Euclidian distance, correlation distance, cosine distance, Manathan distance and Jaccard distance. In the command line or GUI of SPMF, the distance function is specified by using one of these keywords: "euclidian", "correlation", "cosine", "manathan" and "jaccard" as parameter. In this example, the euclidian distance is used.
The ITER specifies how much times the algorithm should repeat a split to keep the best split. If it is set to a high value it should provide better results but it should be more slow. Splits are evaluated using the Squared Sum of Errors (SSE).
What is the output?
Bisecting K-Means groups vectors in clusters according to their similarity. In SPMF, the similarity is defined according to the distance function chosen by the user such as the Euclidian distance. K-Means returns K clusters or less.
Note that running Bisecting K-Means with the same data does not always generate the same result because Bisecting K-Means initializes clusters randomly.
By running Bisecting K-Means on the previous input file, we can obtain the following output file containing 3 clusters:
@ATTRIBUTEDEF=X
@ATTRIBUTEDEF=Y
[Instance1 1.0 1.0][Instance2 0.0 1.0][Instance3 1.0 0.0][Instance12 8.0 2.0][Instance13 9.0 2.0][Instance14 10.0 1.0][Instance16 5.0 9.0][Instance28 9.0 3.0][Instance29 9.0 4.0][Instance30 9.0 5.0]
[Instance9 13.0 9.0][Instance24 15.0 9.5][Instance7 12.0 8.5][Instance8 13.0 8.0][Instance10 13.0 7.0][Instance11 11.0 7.0][Instance18 11.5 8.0][Instance20 13.0 10.0][Instance25 12.0 9.5][Instance23 15.0 10.5]
[Instance4 11.0 12.0][Instance5 11.0 13.0][Instance6 13.0 13.0][Instance17 16.0 16.0][Instance21 12.0 13.0][Instance21 14.0 12.5][Instance22 14.5 11.5][Instance15 7.0 13.0][Instance26 10.5 11.0][Instance27 10.0 10.5]
The output file format is defined as follows. The first few lines indicate the attribute names. Each attribute is specified on a separated line with the keyword "ATTRIBUTEDEF=" followed by the attribute name (a string). Then, the list of clusters is indicated. Each cluster is specified on a separated line, listing the instances contained in the cluster. An instance is a name followed by a list of double values separated by " " and between the "[" and "]" characters.
The clusters found by the algorithm can be viewed visually using the "Cluster Viewer" provided in SPMF. If you are using the graphical interface of SPMF, click the checkbox "Cluster Viewer" before pressing the "Run Algorithm" button. The result will be displayed in the Cluster Viewer.
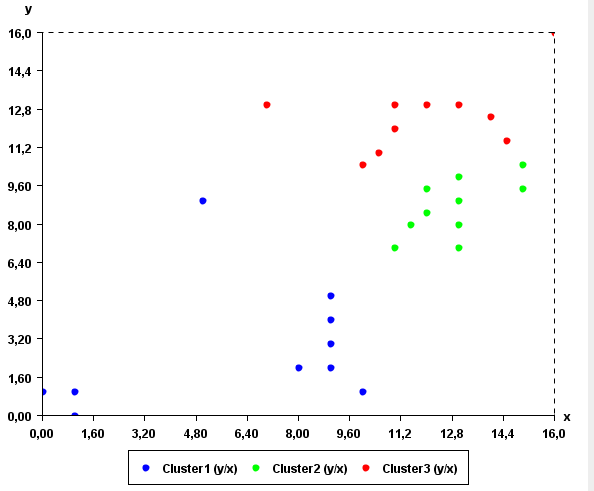
As it can be seen in this example, the result somewhat make sense, as points close to each other are in the same cluster.
Applying Bisecting K-Means to time series
Note that the Bisecting K-Means algorithm implementation in SPMF can also be applied to time series database such as the file contextSAX.txt in the SPMF distribution. To apply this algorithm to time series, it is necessary to set the "separator" parameter of this algorithm to "," since time series files separate values by "," instead of separating by spaces.
Where can I get more information about Bisecting K-Means ?
The original K-Means was proposed by MacQueen in 1967. K-means is one of the most famous data mining algorithm. It is described in almost all data mining books that focus on algorithms, and on many websites. By searching on the web, you will find plenty of resources explaining K-Means.
The Bisecting K-Means algorithms is described in this paper:
A comparison of document clustering techniques", M. Steinbach, G. Karypis and V. Kumar. Workshop on Text Mining, KDD, 2000.